Анализ фильтра низких частот

Моделирование ограничения выходного напряжения производится в выходном блоке путем введения нелинейного сопротивления, как это показано на рисунке 5.

Входной блок и усилительный блок 2 строятся аналогичным образом, как и в линеаризованной динамической модели.

            Рисунок 5 - Моделирование ограничения выходного напряжения

                                     а) схема выходного блока;

                                     б) ВАХ нелинейного сопротивления

 2  Расчетная часть

2.1  Исследование частотных характеристик схемы

Для исследования частотных характеристик необходимо применить линеаризованную схему замещения устройства. Это связано с тем, что в этом случае амплитуда выходной синусоиды достаточно мала для того, чтобы пренебречь нелинейностью.

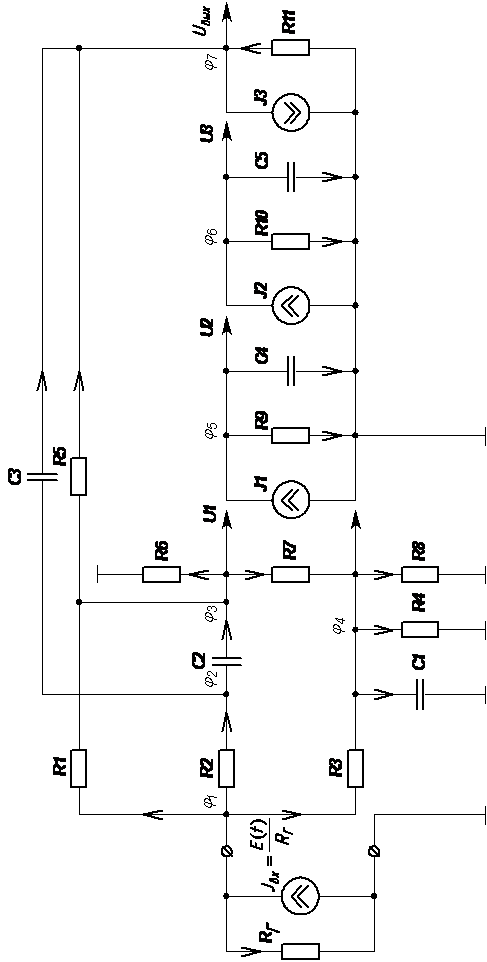
            На рисунке 6 представлена линеаризованная схема замещения устройства, составленная с использованием линеаризованной динамической модели операционного усилителя. В схеме произвольно расставлены направления протекающих токов и обозначены потенциалы узлов. Источник ЭДС на входе заменен на источник тока.

Воспользовавшись I законом Кирхгофа, составляем топологические уравнения для токов узлов.

                                                                        (2.1)

Из системы (2.1) получаем систему дифференциальных уравнений

      (2.2)

            Для практического расчета частотных характеристик обычно применяют отображения Лапласа исходной системы интегрально-дифференциальных (в нашем случае, просто дифференциальных) уравнений в комплексное пространство. Проделаем это с системой (2.2)

            Преобразуем полученную систему следующим образом

            Значения , , , , , , ,  указаны в задании. Найдем значения остальных параметров.

            Примем .

            Из справочника берем значения входных дифференциального и синфазных сопротивлений 140УД7: , . Там же берем значение .

            Усилительный блок 1 моделирует первый полюс. Зададимся значением его частоты .

Согласно (1.1) .

Зададимся значениями  и .

Тогда из (1.2) получим

.

Усилительный блок 2 моделирует второй полюс. Зададимся значением его частоты .

Зададимся значением . Согласно тому, что  находим .

Получаем

.

Источник тока  описывается как .

Выберем в выходном блоке сопротивление =10 Ом. Из соотношения  находим .

Источник тока  описывается как .

Таким образом, получены все исходные значения параметров схемы.

Для получения частотных характеристик устройства воспользуемся математическим пакетом MathCad, так как решение системы (2.3) без применения средств ЭВМ - занятие довольно трудоемкое.

Программа MathCad для построения частотных характеристик представлена в приложении В.

На рисунках 7 и 8 соответственно приведены получившиеся графики АЧХ и ФЧХ фильра.

Рисунок 7 - АЧХ фильтра

Рисунок 8 - ФЧХ фильтра

            Согласно полученным графикам, резонансная частота фильтра .

2.2             Исследование временных характеристик схемы

Для исследования временных характеристик устройства  применим схему замещения фильтра, изображенную на рисунке 6.

Преобразуем систему (2.2) в систему дискретных уравнений

            В данной системе неизвестными являются значения потенциалов .

            Значения потенциалов  известны: вычислены на предыдущем шаге решения системы. Для этого необходимо задаться начальными условиями . При этом данные потенциалы на каждом шаге вычислений играют роль источников тока.

            Таким образом, мы получили линейную систему алгебраических уравнений, решаемую реккурентным способом. На каждом шаге полученную систему можно решить любым методом: начиная от методов Гаусса и Крамера и заканчивая методом LU-факторизации.

Однако, мы воспользуемся средой MathCad. Для этого представим полученную систему в виде

            Рабочий фрагмент программы MathCad для расчета временной характеристики представлен в приложении Г. Описательный фрагмент (задание констант-значений параметров элементов) аналогичен такому же из предыдущей программы.

            Результат выполнения программы представим в виде графика, приведенного на рисунке 9.

            Рисунок 9 - График временной характеристики фильтра

Заключение

             В данной работе была проанализирована предложенная схема фильтра низких частот.

            Для этого использовались такие методы анализа и расчета электронных схем, как математическое моделирование исходной схемы (составление системы уравнений) по разработанной схеме замещения устройства.

            Решение систем уравнений производилось в среде MathCad.

            Результаты выполнения программ MathCad представлены в виде графиков.

Список использованных источников

             1.  Аксенов А.И., Нефедов А.В. Резисторы. Конденсаторы. Справочное пособие. - М.: СОЛОН-Р, 2000. - 240 с.

            2.  Гальперин М.В. Практическая схемотехника в промышленной автоматике. - М.: Энергоатомиздат, 1987. - 320 с.

3.  Титце У., Шенк К. Полупроводниковая схемотехника. Пер. с нем. Под ред. Алексенко А.Г. - М.: МИР, 1983. - 512 с.

4.  Щербаков В.И., Грездов Г.И. Электронные схемы на операционных усилителях. - К.: Технiка, 1983. - 213 с.

         5. http://users.kpi.kharkov.ua - Личная страница доц. каф. ВТП к.т.н. Скороделова В.В.

1	2

Copyright © Radioland. Все права защищены.
Дата публикации: 2004-09-01 (220 Прочтено)