Студентам > Рефераты > Расчет надежности, готовности и ремонтопригодности
Расчет надежности, готовности и ремонтопригодностиСтраница: 1/3
1.Введение
Вычислительной
системой (ВС) будем называть
совокупность вычислительных средств, включающих не менее двух вычислительных
машин или процессов предназначенных для автоматической обработки информации в
соответствии с заданным алгоритмом.
Качеством называется совокупность свойств,
определяющих пригодность использования вычислительной машины или системы , по
назначению. Качеством является совокупностью свойств, поэтому оно оценивается
множеством показателей. Выбор показателей определяется назначением
вычислительной машины или системы, ее структурой, видом избыточности, длительностью
функционирования и т.п. Показатель качества - это вектор, компонентами
которого служат показатели свойств, являющиеся частными показателями качества.
Показатели
качества можно классифицировать по пригодности, оптимальности и превосходству.
Вычислительные машины или системы, удовлетворяюие показателям оптимальности-
являются наилучшими , т.е. обладают наивысшим качеством; удовлетворяющие
показателям превосходства считаются превосходящими по качеству остальные машины
или системы.
При
оценке качества вычислительной системы в процессе ее разработки или
эксплуатации встречаются с двумя трудностями. В большинстве случаев не удается
установить единый обобщенный показатель качества, который позволил бы сравнить
пазличные системы и выбрать наилучшую. Это объясняется тем, что качество
оценивается множеством свойств.
Вторая
трудность состоит в том, что не существует методики установления требований на
показатели качества. Это объясняет тем, что не удается разработать на все
случаи жизни критерия оптимальности системы в смысле ее качества.
Основными
характеристиками вычислительных машин и систем, определяющими их качество,
являются надежность, ремностопригодность, готовность , эффективность.
Надежностью называется свойство технического устройства
сохранять свои характеристики в данных условиях эксплуатации.
Показателями надежности невосстанавливаемых вычислительных машин и систем
могут быть: вероятность безотказной работы  , среднее время безотказной работы T,
частота отказов , среднее время безотказной работы T,
частота отказов   , и интенсивность
отказов , и интенсивность
отказов  . .
Показателями
надежности восстанавлимаемых машин и систем являются : средняя частота отказов  и наработка на отказ и наработка на отказ  . .
Показатели надежности
связаны, между собой зависимостями:
 (1.1) (1.1)



Показатели
надежности невосстанаялияаемых систем могут также характеризовать надежность
восстанавливаемых систем, если оценивается их функционирование до первого
отказа. При этом восстановление отказавших резервных устройств допускается в
прецессе работы машины или системы.
Наличие
больших чисел показателей вовсе не означает, что всегда необходимо оценивать
надежность вычислительной системы по всем показателям.
Наиболее
полно характеризует надежность невосстанаялияаемой системы частота отказов. Это
объясняется тем, что  является
плотностью распределения, а поэтому несет в себе всю информацию о случайном
явлении-времени безотказной работы.Такие характеристики, как вероятность
безотказной работы, интенсивность отказов, среднее время безотказной работы
являются лишь характеристиками распределения и всегда могут быть получены, если
известно является
плотностью распределения, а поэтому несет в себе всю информацию о случайном
явлении-времени безотказной работы.Такие характеристики, как вероятность
безотказной работы, интенсивность отказов, среднее время безотказной работы
являются лишь характеристиками распределения и всегда могут быть получены, если
известно  .
Однако оценивать надежность вычислительной системы частотой отказов в
большинстве случаев нецелесообразно, так как она не обладает достаточной
наглядностью и не входит в другие более общие характеристики качества ВС. Она
используется обычно при определении доверительных вероятностей при обработке
данных статистичесих испытаний технических устройств. .
Однако оценивать надежность вычислительной системы частотой отказов в
большинстве случаев нецелесообразно, так как она не обладает достаточной
наглядностью и не входит в другие более общие характеристики качества ВС. Она
используется обычно при определении доверительных вероятностей при обработке
данных статистичесих испытаний технических устройств.
Интенсивность
и средняя частота отказов – наиболее удобныe характеристики надежности простых
элементов. Это объясняется тем, что интенсивности отказов многих экементов
электроники и вычислительной техники есть величины постоянные и характеризуются
одним числом. Кроме того, по этим характеристики надежности машины и системы.
Среднее
время безотказной работы является достаточно наглядной характеристикой
надежности невосстанавливаемых машин и ВС. Однако применеие этого показателя
нецелесообразно в тех случаях, когда время работы ВС гораздо меньше среднего
времени безотказной работы, закон распределения времени безотказной работы, закон
распределения времени безотказной работы не однопараметрический и для
достаточно полной оценки требуется моменты высших порядков, машина или ВС
резервированы, интенсивность отказов непостоянна, элементы ВС работают не
одновременно.
Ремонтопригодностью называется способность технического устройства к
восстановлению в процессе эксплуатации. Показателями ремонтопригодности
могут быть: вероятность восстановления системы за заданное время  , среднее время
восстановления , среднее время
восстановления  ,
закон распеределения времени восстановления ,
закон распеределения времени восстановления  , интеносивность восстановления , интеносивность восстановления  . .
Вероятность  является интервальным
показателем , является интервальным
показателем ,  -
интегральным, а -
интегральным, а  и и  -точечными
показателями ремонтопригодности. -точечными
показателями ремонтопригодности.
Наиболее
часто для оценки ремонтопригодности ВС применяется среднее время
восстанавления. Эта характеристика наиболее наглядна, она во многом определяет
такой важный показатель качества ВС, как готовность. Она является интегральной,
поэтому обладает следующим недостатком: неполно характеризует
ремонтопригодность ВС, если закон распределения времени восстаналения не
однопараметричный и для оценки ремонтопригодности требуется знание моментов
высшего порядка.
Важнейшей
характеристикой ремонтопригодности технических устройств вычислительных машин и
систем является интенсивность их восстановления. Это объясняется тем, что
большинство показателей качества ВС в процессеих проектирования вычисляются
через интенсивности восстановления их устройств.
Готовностью называется способность технического устройства быть
готовы м к действию в любой момент времени. Она зависит от надежности и от
ремонтопригодности ВС.Чем выше надежность и ремонтопригодность ,тем выше
готовность.Показателями готовности могут быть: функция готовности  и коэффициент
готовности и коэффициент
готовности  . .
Функция готовности есть
вероятность того, что в любой момент времени 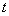 система готова к действию. Эта
характеристика обычно имеет вид, показанный на рис. 1.1. Из рисунка видно, что система готова к действию. Эта
характеристика обычно имеет вид, показанный на рис. 1.1. Из рисунка видно, что  =1, т.е. считается, что
ВС начинает эксплуатироваться исправной. С ростом =1, т.е. считается, что
ВС начинает эксплуатироваться исправной. С ростом 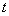  убывает и при убывает и при  функция готовности стремится к
постоянной, отличной от нуля величине, которая является финальной вероятностью
и называется коэффициентом готовности. Таким образом, между функцией и
коэффициентом готовности существует зависимость функция готовности стремится к
постоянной, отличной от нуля величине, которая является финальной вероятностью
и называется коэффициентом готовности. Таким образом, между функцией и
коэффициентом готовности существует зависимость  . (1.2) . (1.2)

Функция
и коэффициент готовности являются характеристиками точечными. Эта означает, что
ордината  ,
показанная на рис. 1.1, есть вероятность того, что в момент времени ,
показанная на рис. 1.1, есть вероятность того, что в момент времени 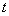 система исправна. До
момента система исправна. До
момента 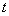 она
могла сколь угодно раз отказывать и ремонтироваться. она
могла сколь угодно раз отказывать и ремонтироваться.
Коэффициент
готовности легко вычисляется, если известны интегральные характеристики
надежности и ремонтопригодности
 (1.3) (1.3)
где  -наработка на отказ
вычислительной системы; -наработка на отказ
вычислительной системы;  - среднее время восстановления ВС. - среднее время восстановления ВС.
Функция
готвности  может
иметь возрастающей функции или колебательной. В случае возрастающей функции,
когда в начале эксплуатации Вс имеет неисправные резервные устройства может
иметь возрастающей функции или колебательной. В случае возрастающей функции,
когда в начале эксплуатации Вс имеет неисправные резервные устройства  . .
Если же анализ готовности
системы начинается с момента времени, когда система вообще неисправна и
ремотируется, то  . .
Колебательный процесс
изменения функции готовности наблюдается при обслуживании ВС с определенным
видом приоритета и длительностью времени восстановления.
Независимо от
вида кривых  финальная
вероятность для данной системы всегда постоянна и имеет одно и то же значение,
определяемое выражением (1.3), т.е. коэффициент готовности не зависит от
начального состояния ВС, из которого начинается ее эксплуатация. финальная
вероятность для данной системы всегда постоянна и имеет одно и то же значение,
определяемое выражением (1.3), т.е. коэффициент готовности не зависит от
начального состояния ВС, из которого начинается ее эксплуатация.
2. Надежность, готовность и
ремонтопригодность технических средств и вычислительных комплексов
2.1 Граф состояний вычислительной системы
Вычислительная
система в процессе функционирования может находиться в большом числе различных
состояний. Например, все устройства системы исправны или i-е (i=1,2,…,N)
устройств отказало, а остальные исправны, или i-е и j-е устройства отказали, а
остальные исправны и т.п. При восстановлении отказавших устройств система в
дискретные моменты времени переходит из одного состояния в другое. В процессе
длительной экслпуатации она может побывать в каждом из возможных состояний
многократно. Тогда ее функционирование может быть описано графов, узлы которого
соответствуют состояниям системы, а ветви указывают все возможные переходы из
состояния.Если в графе имеется n узлов, то среди них будет k узлов, отражающих
отказовые состояния, и n-k узлов, отражающих исправные состояния.
Часто
интересуются функционированием системы до некоторого l–го состояния , например
до первого ее отказа. Тогда l-е состояние называется поглощающим. Система,
попавшая в l-е состояние, уже не может перейти в другие, и в графе отсутствуют
ветви переходов из этого состояния (экран).
Вид
графа зависит от структуры системы (схемы расчета надежности), числа
обслуживающих бригад и дисциплины обслуживания. Обычно узлы графа нумеруются и
отмечаются (например, крестом) те, которые соответствуют отказвым состояниям
системы. На графе также указываются все интенсивности переходов.
 1
1
 
 
N
2
 0 0 
Рис.2.1 Граф состояний восстанавливаемой нерезервированной машины
Сформулируем
ряд важных свойств графов состояний:
1.Граф состояний полностью
описывает функционирование ВС как системы массового обслуживание. Вид графа
определяется структурной схемой системы, надежностью и ремнотопригодностью
элементов, а также дисциплиной обслуживания системы. На основании этого
свойства можно утверждать, что все количественные характеристики надежности,
готовности и ремонтопригодности ВС могут быть определены непосредственно из
графа ее состояний.
2.Граф, не содержащий
поглощающих состояний, описывает поведение системы при неограниченном ремонте.
3.Число узлов графа
состояний может быть больше или меньше 2n где n - число элементов
структурной схемы. Это объясняется тем, что граф описывает поведение ВС
совместно с обслуживающим органом.
4.Функционирование ВС при
обратном приоритете обслуживания отказавших элементов описывается графом типа
дерева.
2.2 Описание функционирования вычислительной системы
дифференциальными уравнениями
Составить
систему дифференциальных уравнений для определения количественных характеристик
надежности, готовности и ремонтопригодности ВС можно по виду графа состояний
системы. Сформулируем первоначально правило состовления уравнений для
определения вероятности пребывания системы в i-м состоянии в момент времени t.
Часть графа с состотянием i-1,i,i+1 показана на рис.2.2 Тогда дифференциальное
уравнение для вероятности  пребывания системы в i-м состоянии в
момент времени t будет иметь вид: пребывания системы в i-м состоянии в
момент времени t будет иметь вид:

Из уравнения видно, что
слева пишется производная по времени от вероятности пребывания системы, в i-м
состоянии в момент времени t, а справа – сумма произведений интенсивностей
переходов из всех соседних состояний в i-е состояние и из i-го – во все
соседние на соответствующие вероятности состояний. Знаки в правой части
уравнения определяются по направлению стрелок в ветвях графа. Если стрелка
направлена в i-е состояние, то при соответсвующей ей интенсивности перехода
ставится знак “+”, в противном случае – знак “-”. Это правило справедливо при
любом числе соседних с i-м состояний.
 
| 
 Главная
Главная
 Схемы
Схемы
 Студентам
Студентам
 Программы
Программы
 Поиск
Поиск
 Top50
Top50

 Главная
Главная
 Схемы
Схемы
 Студентам
Студентам
 Программы
Программы
 Поиск
Поиск
 Top50
Top50