Проектирование АЛУ для сложения двоично-десятичных чисел

Содержание

Введение 2

1 Постановка задачи 3

1.1Общие сведения о работе сумматора. Принцип построения сумматоров 3

1.2 Запись десятичных чисел 6

1.3Суммирование двоично-десятичных чисел 7

2 Построение АЛУ 8

2.1 Построение функциональной и структурной схем АЛУ 8

2.2 Описание работы принципиальной схемы 8

3 Описание элементной базы АЛУ 11

Список литературы 12

Введение

В настоящее время – время компьютерных технологий, в нашу жизнь всё больше и больше входят и успешно применяются всевозможные «умные вещи», например автоматические стиральные машины, СВЧ печи, DVD проигрыватели тому подобные предметы. Все они предназначены для того, чтобы, как можно больше облегчить наши повседневные хлопоты и одновременно уменьшить время, затрачиваемое на рутинные бытовые заботы. Однако не все знают, что работа этих устройств не просто какое-то волшебство, а свет инженерной мысли их создателей. Также, не все знают, что команды, выполняемые этими приборами, подразумевают работу с двоичными числами, которые представляются в виде кодов выполняемых операций. Например, мы нажимаем кнопку изменения уровня громкости на пульте управления телевизора, и видим на экране шкалу, которая увеличивается (уменьшается) в зависимости от выбранной кнопки, одновременно вы слышим изменение звучания. Эти изменения вызваны тем, что определённая комбинация представленная в двоичном коде передаётся на управляющие органы телевизора, тем самым выполняет необходимое нам действие.

1 Постановка задачи

1.1Общие сведения о работе сумматора. Принцип построения сумматоров

Сумматор осуществляет арифметическое суммирование n-разрядных кодов X=(x(n-1), ,x0) и Y=(y(n-1), ,y0). Правила сложения двух одноразрядных двоичных чисел:

0 (+) 0 = 0

0 (+) 1 = 1 (+) 0 = 1

1 (+) 1 = 0 и перенос 1 в старший разряд.

Операция (+) называется - сумма по модулю два. Устройство реализующее эти правила называется одноразрядным полусумматором и имеет два входа и два выхода. Сложение трех одноразрядных чисел производится следующим образом:

0 (+) 0 (+) 0 = 0

0 (+) 0 (+) 1 = 1

0 (+) 1 (+) 1 = 0 и перенос 1 в старший разряд

1 (+) 1 (+) 1 = 1 и перенос 1 в старший разряд.

Устройство реализующее эти правила называется одноразрядным полным сумматором (ОПС) и имеет три входа и два выхода. Таблица истинности ОПС приведена на рис.1, слева.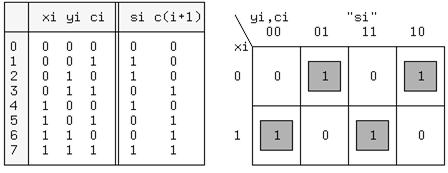

Рисунок 1

xi,yi - одноименные двоичные разряды чисел X и Y, ci - перенос из предыдущего разряда, si - частичная сумма по модулю два и c(i+1) - перенос в следующий разряд. Значения c(i+1) совпадают со значениями функции мажоритарности, поэтому воспользуемся готовым решением:

c(i+1) = xi*yi + xi*ci + yi*ci. (1)

Таблица Карно для si приведена на рис.1 справа. Из таблицы находим: si = xi*~yi*~ci + ~xi*~yi*ci + xi*yi*ci+ ~xi*yi*~ci = ~yi(xi*~ci + ~xi*ci) + yi(xi*ci + ~xi*~ci) = ~yi(xi (+) ci) + yi(xi*ci + ~xi*~ci). Выражение в последней скобке необходимо преобразовать, используя соотношение двойственности.

xi*ci + ~xi*~ci = ~(xi*ci) * ~(~xi*~ci) = (~xi+~ci) *(xi+ci)= ~xi*xi + ~xi*ci + ~ci*xi + ~ci*ci = ~xi*ci + xi*~ci = ~(xi (+) ci) = ~F6 = F9,

где F6=x1 (+) x0 - исключающее ИЛИ,

F9= ~(x1 (+) x0) исключающее - ИЛИ-НЕ

С учетом последнего выражения

si = ~yi(xi (+) ci) + yi~(xi (+) ci) =

yi (+) (xi (+) ci) = yi (+) xi (+) ci. (2)

Схема полного одноразрядного сумматора соответствующая уравнениям (1) и (2) и её условное обозначение приведены на рисунке 2.

Рисунок 2

Сумматор с последовательным переносом для сложения n- разрядных двоичных чисел показан на схеме (рис.3.). К его недостатку относится большое время задержки, в наихудшем случае, когда от сложения x0,y0 возникает сквозной перенос через все разряды до выхода s(n-1). При двухъярусной схеме одноразрядного сумматора, задержка сигнала от входов до выходов составит 2tзд.р., если считать задержку в каждом ярусе одинаковой. Суммарная величина задержки будет равна:

tзд.р.посл.сумматора = n*2tзд.р. (3)

При сложении многоразрядных чисел задержка выходного сигнала на выходе последнего разряда становится недопустимо большой.

Рисунок 3

В ЭВМ сумматор является центральным узлом арифметико-логического устройства (АЛУ) и от его быстродействия зависит производительность компьютера. Поэтому применяются сумматоры с параллельной схемой переноса. Выражение (1) для младшего разряда можно преобразовать, используя тождество для функции ИЛИ: x + y = ~x*y + x*~y + xy. В правой части равенства совершенной дизъюнктивной нормальной формой (СДНФ) выражения (4) функции ИЛИ. Тогда

c1 = x0*y0 + x0*c0 + y0*c0 = x0*y0 + c0(x0 + y0) =

x0*y0 + c0(~x0*y0 + x0*~y0 + x0*y0) =

x0*y0(с0 +1) + c0(~x0*y0 + x0*~y0) =

x0*y0 + с0(x0 (+) y0). (5)

Уравнениям (2) и (5) соответствует схема на рис.4

Рисунок 4

Если в каждом разряде сумматора использовать такой одноразрядный сумматор, то никакого выигрыша в скорости не будет. Узел, обведенный точками, называется узлом переноса (УП), а функции gi и pi называются функциями генерации переноса и распространения переноса. С учетом этого можно записать:

c1 = g0 + p0*c0, с2 = g1 + p1*c1 = (6)

= g1 + p1*g0 + p1*p0*c0, (7)

с3 = g2 + p2*c2 = (8)

= g2 + p2*g1 + p2*p1*g0 + p2*p1*p0*c0, (9)

, и так далее. Выражения (6, 8) - это еще последовательный сумматор, т.к. c3 зависит от c2, c2 зависит от c1, а c1 зависит от c0. Выражения (7, 9) соответствуют уже параллельному, т.к. величина ci снимается с выхода предыдущего разряда, в котором она формируется параллельно из всех первичных переменных. Схемы узлов переноса УП1 и УП2 приведены на рис.5.

Рисунок 5

Из рис.4 и 5 видно, что узел сложения в каждом разряде остается неизменным, а изменяется только узел переноса, причем задержка сигнала от входов xi, yi до c(i+1) остается неизменной и для 3-ярусной схемы равна 3tзд.р Суммарная задержка в каждом разряде увеличится на время прохождения сигнала от входа ci до si, т.е. на величину tзд.р., и составит: tзд.р.паралл.сумматора = 4tзд.р. независимо от количества разрядов. За это приходится платить усложнением узла переноса от разряда к разряду.

1.2 Запись десятичных чисел

1	2	3