Студентам > Курсовые > Расчет переходных процессов в линейных цепях с сосредоточенными параметрами
Расчет переходных процессов в линейных цепях с сосредоточенными параметрамиСтраница: 2/3
50= 

Искомое выражение для тока второй ветви:
 (А); (А);
Определение  : :
Согласно уравнению (3)  , ,  (В); (В);
Из системы (1): 

  
II. Операторный метод расчета
1) Составляется операторная схема замещения исходной электрической цепи (Рис.1) для времени  . При этом все известные и неизвестные функции заменяются изображениями. Для нахождения параметров дополнительных источников операторной схемы замещения с помощью законов коммутации определяются независимые начальные условия (НУ): . При этом все известные и неизвестные функции заменяются изображениями. Для нахождения параметров дополнительных источников операторной схемы замещения с помощью законов коммутации определяются независимые начальные условия (НУ): 
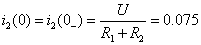 (А); (А);  (В). (В).
2) Находится изображение искомого тока. Операторная схема замещения содержит 3 источника в разных ветвях: основной и два дополнительных. Поэтому для нахождения изображения тока второй ветви воспользуемся законами Кирхгофа в операторной форме:
  (7) (7)
Подставим выражения для начальных условий в систему (7). Первое уравнение системы подставим во второе, выразим ток  и подставим его в третье уравнение системы, в результате получили одно уравнение с одним неизвестным и подставим его в третье уравнение системы, в результате получили одно уравнение с одним неизвестным  . .
 

3) По найденному изображению определяется оригинал. Для нахождения корней приравнивается к нулю выражение  : :
 ; ;  ; ;  ; ;
 (1/с); (1/с);  (рад/с). (рад/с).

 ; ;
 ; ;
 ; где ; где  
 ; ;
 (А). (А).
Искомое выражение для тока  : :
 (А). (А).
4) Аналогично найдем ток в первой  из системы уравнений (7). из системы уравнений (7).
Подставим выражения для начальных условий в систему (7). Найденное выражение для тока  в пункте (3) подставим во второе уравнение системы (7): в пункте (3) подставим во второе уравнение системы (7):
 ; ;

 ; ;  ; ;  ; ;
 (1/с); (1/с);  (рад/с). (рад/с).


 ; ;
 ; где ; где   ; ;
 
 ; ;
Искомое выражение для тока  : :

5) Найдем напряжения  : :

 ; ;

 ; ;  ; ;  ; ;
 (1/с); (1/с);  (рад/с). (рад/с).

 
 ; ;
 ; где ; где   ; ;


Искомое выражение:
 (В); (В);
6)
Найдем ток третьей ветви  : :

 ; ;
 ; ;  ; ;  ; ;
| 
 Главная
Главная
 Схемы
Схемы
 Студентам
Студентам
 Программы
Программы
 Поиск
Поиск
 Top50
Top50

 Главная
Главная
 Схемы
Схемы
 Студентам
Студентам
 Программы
Программы
 Поиск
Поиск
 Top50
Top50