Студентам > Курсовые > Метод конечных разностей или метод сеток
Метод конечных разностей или метод сетокСтраница: 1/4
ВВЕДЕНИЕ
Значительнаое
число задач физики и техники приводят к дифференциальным уравнениям в частных
прозводных (уравнения математической физики). Установившиеся процессы различной
физической природы описываются уравнениями эллиптического типа.
Точные
решения краевых задач для эллиптических уравнений удаётся получить лишь в
частных случаях. Поэтому эти задачи решают в основном приближённо. Одним из
наиболее универсальных и эффективных методов, получивших в настоящее время
широкое распространение для приближённого решения уравнений математической
физики, является метод конечных разностей или метод сеток.
Суть
метода состоит в следующем. Область непрерывного изменения аргументов,
заменяется дискретным множеством точек (узлов), которое называется сеткой или решёткой.
Вместо функции непрерывного аргумента рассматриваются функции дискретного
аргумента, определённые в узлах сетки и называемые сеточными функциями.
Производные, входящие в дифференциальное уравнение и граничные условия,
заменяются разностными производными, при этом краевая задача для
дифференциального уравнения заменяется системой линейных или нелинейных
алгебраических уравнений (сеточных или разностных уравнений). Такие системы
часто называют разностными схемами. И эти схемы решаются относительно неизвестной
сеточной функции.
Далее
мы будем рассматривать применение итерационного метода Зейделя для вычисления
неизвестной сеточной функции в краевой задаче с неоднородным бигармоническим
уравнением.
ПОСТАНОВКА ЗАДАЧИ
Пусть у нас есть
бигармоническое уравнение :
 2 2
U = f
Заданное на области G={ (x,y) :
0<=x<=a, 0<=y<=b }. Пусть также заданы краевые условия на
границе области G .
  U =
0 Y U =
0 Y
x=0 b
  Uxxx =
0 Uxxx =
0
x=0
G
 Ux = 0 Ux = 0
x=a
  Uxxx = 0 0
a X Uxxx = 0 0
a X
x=a
  U =
0 U = 0 U =
0 U = 0
y=0
y=b
   Uy =
0 Uxx + Uyy = 0 Uy =
0 Uxx + Uyy = 0
y=0
y=b y=b
Надо
решить эту задачу численно.
  Для решения будем
использовать итерационный метод Зейделя для решения сеточных задач. Для решения будем
использовать итерационный метод Зейделя для решения сеточных задач.
 По нашей области G
построим равномерные сетки Wx и Wy с шагами
hx и hy соответственно . По нашей области G
построим равномерные сетки Wx и Wy с шагами
hx и hy соответственно .
 Wx={ x(i)=ihx,
i=0,1...N,
hxN=a } Wx={ x(i)=ihx,
i=0,1...N,
hxN=a }
 Wy={ y(j)=jhy,
j=0,1...M, hyM=b } Wy={ y(j)=jhy,
j=0,1...M, hyM=b }
Множество узлов Uij=(x(i),y(j)) имеющих координаты на
плоскости х(i),y(j) называется сеткой в прямоугольнике G
и обозначается :
W={ Uij=(ihx,jhy), i=0,1...N, j=0,1...M, hxN=a, hyM=b }
Сетка W очевидно состоит из точек
пересечения прямых x=x(i) и y=y(j).
  Пусть задана сетка W.Множество
всех сеточных функций заданных на W образует векторное пространство с
определённом на нём сложениемфункций и умножением функции на число. На
пространстве сеточных функций можно определитьразностные или сеточные
операторы. 0ператор A преобразующий сеточную функцию
U в сеточную функцию f=AU называется разностным
или сеточным оператором. Множество узлов сетки используемое при написании
разностного оператора в узле сетки называется шаблоном этого оператора. Пусть задана сетка W.Множество
всех сеточных функций заданных на W образует векторное пространство с
определённом на нём сложениемфункций и умножением функции на число. На
пространстве сеточных функций можно определитьразностные или сеточные
операторы. 0ператор A преобразующий сеточную функцию
U в сеточную функцию f=AU называется разностным
или сеточным оператором. Множество узлов сетки используемое при написании
разностного оператора в узле сетки называется шаблоном этого оператора.
Простейшим разностным
оператором является оператор дифференцирования сеточной функции, который
порождает разностные производные. Пусть W - сетка с шагом h введённая на R т.е.
W={Xi=a+ih, i=0, + 1, +
2...}
Тогда разностные производные первого порядка для
сеточной функции Yi=Y(Xi) , Xi из W, определяется по
формулам :
L1Yi = Yi - Yi-1 , L2Yi=L1Yi+1
h
и называются соответственно левой и правой
производной. Используется так же центральная производная :
L3Yi=Yi+1 - Yi-1 = (L1+L2)Yi
2h 2
Разностные операторы A1, A2, A3 имеют шаблоны состоящие
2х точек и используются при апроксимации первой производной Lu=u’ . Разностные производные n-ого порядка определяются
как сеточные функции получаемые путём вычисления первой разностной производной
от функции, являющейся разностной производной n-1 порядка, например :
Yxxi=Yxi+1 - Yxi = Yi-1-2Yi+Yi+1
2
h h
Yxxi= Yxi+1-Yxi-1 = Yi-2 - 2Yi+Yi+ 2
2
2h 4h
которые используются при апроксимации второй
производной. Соответствующие разностные операторы имеют 3х точечный шаблон.
Анологично не
представляет труда определить разностные производные от сеточных функций
нескольких переменных.
Аппроксомируем нашу
задачу с помощью разностных производных. И применим к получившейся сеточной
задаче метод Зейделя.
МЕТОД ЗЕЙДЕЛЯ
Одним из способов
решения сеточных уравнений является итерационный метод Зейделя.
Пусть нам дана система
линейных уравнений :
AU = f
или в развёрнутом виде :
M
 aijUj = fi
, i=1,2...M
aijUj = fi
, i=1,2...M
i=1
Итерационный метод
Зейделя в предположении что диагональные элементы матрицы А=(aij) отличны от нуля (aii<>0) записывается в следующем
виде :
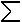 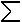 i
(k+1) M (k) i
(k+1) M (k)
aijYj
+ aijYj = fi ,
i=1,2...M
j=1
j=i+1
(k)
где Yj - jая компонента
итерационного приближения номера k. В качестве начального приближения выбирается
произвольный вектор.
Определение (k+1)-ой итерации начинается
с i=1
(k+1)
M (k)
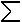 a11Y1 = - a1jYj +f1 a11Y1 = - a1jYj +f1
j=2
(k+1)
Так как a11<>0 то отсюда найдём Y1. И для i=2 получим :
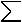 (k+1) (k+1) M (k) (k+1) (k+1) M (k)
a22Y2 = - a21Y1 - a2jYj + f2
j=3
(k+1)
(k+1) (k+1) (k+1)
Пусть уже найдены Y1 , Y2 ... Yi-1 . Тогда Yi находится из уравнения
:
 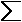 (k+1)
i-1 (k+1) M (k) (k+1)
i-1 (k+1) M (k)
aiiYi =
- aijYj
- aijYj + fi
(*)
j=1
j=i+1
Из формулы (*)
видно , что алгоритм метода Зейделя черезвычайно прост. Найденное по формуле (*)
значение Yi размещается на месте Yi.
Оценим
число арифметических действий, которое требуется для реализации одного
итерационного шага. Если все aij не равны нулю, то
вычисления по формуле (*) требуют M-1 операций
умножения и одного деления. Поэтому реализация
2
одного шага
осуществляется за 2M - M арифметических действий.
Если
отлично от нуля лишь m элементов, а именно эта ситуация имеет место для
сеточных эллиптических уравнений, то на реализацию итерационного шага
потребуется 2Mm-M действий т.е. число
действий пропорционально числу неизвестных M.
Запишем
теперь метод Зейделя в матричной форме. Для этого представим матрицу
A в виде суммы
диагональной, нижней треугольной и верхней треугольной матриц :
A = D + L + U
где
| 
 Главная
Главная
 Схемы
Схемы
 Студентам
Студентам
 Программы
Программы
 Поиск
Поиск
 Top50
Top50

 Главная
Главная
 Схемы
Схемы
 Студентам
Студентам
 Программы
Программы
 Поиск
Поиск
 Top50
Top50