Студентам > Дипломные работы > Двухосный индикаторный стабилизатор телекамер на ВОГ
Двухосный индикаторный стабилизатор телекамер на ВОГСтраница: 1/10
Исследование влияния нежесткостей элементов гиростабилизатора на его
устойчивость.
Анализ устойчивости
ГС с нежесткими наружной рамой, креплением статора двигателя стабилизации к
раме, с нежесткими редуктором и связью платформы с объектом стабилизации, проводим
основываясь на следующей физической модели:
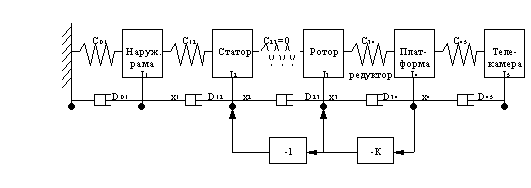
Рис.
1.
здесь Ji -
момент инерции i-го элемента;
Ci,j -
коэффициент упругости;
Di,j -
коэфф. демпфирования между i и j
элементами;
K -
коэффициент передачи цепи обратной
связи.
Оценку влияния
каждого из входящих в модель элементов (Ji,Ci,j,Di,j)
выполняем на основе анализа поведения ЛАХ разомкнутой системы, при вариациях Ji,Ci,j,Di,j.
Уравнения движения
каждого из элементов модели в общем виде могут быть представлены следующим
образом:
Ji×xi''+Di-1,i×(xi'-xi-1')-Di,i+1×(xi+1'-xi')+Ci-1,i× (xi-xi-1)-Ci,i+1×(xi+1 - xi)
= Мi (1)
где Мi -
внешний момент действующий на i-й элемент;
xi,xi',
xi''- перемещение, скорость и ускорение i-го
элемента.
Расписав уравнение
(1) для каждого элемента, получим следующюю систему уравнений движения модели:
J1×x1''+D01×(x1'-x0')-D12×(x2'-x1')+C01×(x1-x0)-C12×(x2-x1)= М1
J2×x2''+D12×(x2'-x1')-D23×(x3'-x2')+C12×(x2-x1)-C23×(x3-x2)= М2
J3×x3''+D23×(x3'-x2')-D34×(x4'-x3')+C23×(x3-x2)-C34×(x4-x3)= М3
(2)
J4×x4''+D34×(x4'-x3')-D45×(x5'-x4')+C34×(x4-x3)-C45× (x5-x4)= М4
J5×x5''+D45×(x5'-x4')-D56×(x6'-x5')+C45×(x5-x4)-C56×(x6-x5)= М5
Раскрыв в (2) скобки
и преобразовав получаем следующий вид уравнений движения модели.
-D01×x0'-C01×x0+J1×x1''+(D01+D12)×x1'+(C01+C12)×x1-D34×x2'-
-C12×x2= М1
-D12×x1'-C12×x1+J2×x2''+(D23+D12)×x2'+(C12+C23)×x2-D23×x3'-
-C23×x3= М2
-D23×x2'-C23×x2+J3×x3''+(D23+D34)×x3'+(C23+C34)×x3-D34×x4'-
-C34×x4=М3 (3)
-D34×x3'-C34×x3+J4×x4''+(D34+D45)×x4'+(C34+C45)×x4-D45×x5'-
-C45×x5= М4
-D45×x4'-C45×x4+J5×x5''+(D45+D56)×x5'+(C45+C56)×x5-D56×x6'-
-C56×x6= М5
Переписав (3) в
операторной форме получаем уравнения движения модели в следующем виде.
-(D01×s+C01)×x0+(J1×s2+(D01+D12)×s+(C01+C12))×x1 -
-(D12×s+C12)×x2= М1
-(D12×s+C12)×x1+(J2×s2+(D12+D23)×s+(C12+C23))×x2-
-(D23×s+C23)×x3= К×x4
-(D23×s+C23)×x2+(J3×s2+(D23+D34)×s+(C23+C34))×x3-
-(D34×s+C34)×x4=-К×x4
-(D34×s+C34)×x3+(J4×s2+(D34+D45)×s+(C34+C45))×x4-
-(D45×s+C45)×x5= М4 (4)
-(D45×s+C45)×x4+(J5×s2+(D45+D56)×s+(C45+C56))×x5-
-(D56×s+C56)×x6= М5
Для нахождения
передаточной функции разомкнутой системы по управляющему воздействию Wp(s)
составим два определителя: главный - D, и характеризующий входное воздействие D1, с учетом того, что x0=0;
D56=0; C56=0; C23=0.
a11 a12 0 0 0
a21 a22 a23 0 0
D= 0 a32 a33 a34 0 (5)
0 0 a43 a44 a45
0 0 0 a54 a55
где a11 = J1×s2+(D01+D12)×s+C01+C12
a12 = -D12×s-C12
a21 = a12
a22 = J2×s2+(D12+D23)×s+C12
a23 = -D23×s
a32 = a23
a33 = J3×s2+(D23+D34)×s+C34
a34 = -D34×s-C34
a43 = a34
a44 = J4×s2+(D34+D45)×s+C34+C45
a45 = -D45×s-C45
a54 = a45
a55 = J5×s2+D45×s+C45
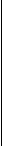 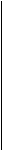 a11 a12 0 0 0 a11 a12 0 0 0
a21 a22 a23
-K×x4 0
D1= 0 a32 a33
K×x4 0 (6)
0 0 a43 0 a45
0 0 0 0 a55
Передаточная функция
разомкнутой системы определяется как:
 D1 -K×(b7×s7+....+b1×s+b0)×x4 D1 -K×(b7×s7+....+b1×s+b0)×x4
  Wp(s) = =
(7) Wp(s) = =
(7)
 D×x4 s×(a9×s9+....+a1×s+a0)×x4 D×x4 s×(a9×s9+....+a1×s+a0)×x4
Коэффициенты ai,
bi полиномов числителя и знаменателя передаточной функции Wp(s)
выражаются через параметры элементов модели следующим образом:
(8)
a9=J1J2J3J4J5
a8=D01J2J3J4J5+D12J3J4J5(J1+J2)+J1(D23J4J5(J2+J3)+J2(D34J5(J3+J4)+D45J3(J4+J5)))
a7=C01J2J3J4J5+C12J3J4J5(J1+J2)+C34J1J2(J3J5+J4J5)+C45J1J2J3(J4+J5)+D01(D12J3J4J5+D23J4J5(J2+J3)+J2(D34J5(J3+J4)+D45J3(J4+J5)))+D12(D23J4J5(J1+J2+J3)+(J1+J2)(D34J5(J3+J4)+D45J3(J4+J5)))+J1(D23(D34J5(J2+J3+J4)+D45(J4+J5)(J2+J3))+D34D45J2(J3+J4+J5))
a6=C01(D12J3J4J5+D23J4J5(J2+J3)+J2(D34J5(J3+J4)+D45J3(J4+J5)))+C12(D01J3J4J5+D23J4J5(J1+J2+J3)+(J1+J2)(D34J5(J3+J4)+D45J3(J4+J5)))+C34(D01J2(J3J5+J4J5)+D12J5(J3+J4)(J1+J2)+J1(D23J5(J2+J3+J4)+D45J2(J3+J4+J5)))+C45(D01J2J3(J4+J5)+D12J3(J4+J5)(J1+J2)+J1(D23(J4+J5)(J2+J3)+D34J2(J3+J4+J5)))+D01(D12(D23J4J5+D34(J3J5+J4J5)+D45J3(J4+J5))+D23(D34(J2J5+J3J5+J4J5)+D45(J4+J5)(J2+J3))+D34D45J2(J3+J4+J5))+D12(D23(D34(J1J5+J2J5+J3J5+J4J5)+D45(J4+J5)(J1+J2+J3))+D34D45(J3+J4+J5)(J1+J2))+D23D34D45J1(J2+J3+J4+J5)
a5=C01(C12J3J4J5+C34J2(J3J5+J4J5)+C45J2J3(J4+J5)+D12(D23J4J5+D34(J3J5+J4J5)+D45J3(J4+J5))+D23(D34(J2J5+J3J5+J4J5)+D45(J4+J5)(J2+J3))+D34D45J2(J3+J4+J5))+C12(C34J5(J3+J4)(J1+J2)+C45J3(J4+J5)(J1+J2)+D01(D23J4J5+D34(J3J5+J4J5)+D45J3(J4+J5))+D23(D34(J1J5+J2J5+J3J5+J4J5)+D45(J4+J5)(J1+J2+J3))+D34D45(J3+J4+J5)(J1+J2))+C34(C45J1J2(J3+J4+J5)+D01(D12(J3J5+J4J5)+D23(J2J5+J3J5+J4J5)+D45J2(J3+J4+J5))+D12(D23(J1J5+J2J5+J3J5+J4J5)+D45(J3+J4+J5)(J1+J2))+D23D45J1(J2+J3+J4+J5))+C45(D01(D12J3(J4+J5)+D23(J2(J4+J5)+J3(J4+J5))+D34J2(J3+J4+J5))+D12(D23(J1(J4+J5)+J2(J4+J5)+J3(J4+J5))+D34(J3+J4+J5)(J1+J2))+D23D34J1(J2+J3+J4+J5))+D01(D12(D23(D34J5+D45(J4+J5))+D34D45(J3+J4+J5))+D23D34D45(J2+J3+J4+J5))+D12D23D34D45(J1+J2+J3+J4+J5)
a4=C01(C12(D23J4J5+D34(J3J5+J4J5)+D45J3(J4+J5))+C34(D12(J3J5+J4J5)+D23(J2J5+J3J5+J4J5)+D45J2(J3+J4+J5))+C45(D12J3(J4+J5)+D23(J2(J4+J5)+J3(J4+J5))+D34J2(J3+J4+J5))+D12(D23(D34J5+D45(J4+J5))+D34D45(J3+J4+J5))+D23D34D45(J2+J3+J4+J5))+C12(C34(D01(J3J5+J4J5)+D23(J1J5+J2J5+J3J5+J4J5)+D45(J3+J4+J5)(J1+J2))+C45(D01J3(J4+J5)+D23(J1(J4+J5)+J2(J4+J5)+J3(J4+J5))+D34(J3+J4+J5)(J1+J2))+D01(D23(D34J5+D45(J4+J5))+D34D45(J3+J4+J5))+D23D34D45(J1+J2+J3+J4+J5))+C34(C45(D01J2(J3+J4+J5)+D12(J1(J3+J4+J5)+J2(J3+J4+J5))+D23J1(J2+J3+J4+J5))+D01(D12(D23J5+D45(J3+J4+J5))+D23D45(J2+J3+J4+J5))+D12D23D45(J1+J2+J3+J4+J5))+C45(D01(D12(D23(J4+J5)+D34(J3+J4+J5))+D23D34(J2+J3+J4+J5))+D12D23D34(J1+J2+J3+J4+J5))+D01D12D23D34D45
a3=C01(C12(C34(J3J5+J4J5)+C45J3(J4+J5)+D23(D34J5+D45(J4+J5))+D34D45(J3+J4+J5))+C34(C45J2(J3+J4+J5)+D12(D23J5+D45(J3+J4+J5))+D23D45(J2+J3+J4+J5))+C45(D12(D23(J4+J5)+D34(J3+J4+J5))+D23D34(J2+J3+J4+J5))+D12D23D34D45)+C12(C34(C45(J1(J3+J4+J5)+J2(J3+J4+J5))+D01(D23J5+D45(J3+J4+J5))+D23D45(J1+J2+J3+J4+J5))+C45(D01(D23(J4+J5)+D34(J3+J4+J5))+D23D34(J1+J2+J3+J4+J5))+D01D23D34D45)+C34(C45(D01(D12(J3+J4+J5)+D23(J2+J3+J4+J5))+D12D23(J1+J2+J3+J4+J5))+D01D12D23D45)+C45D01D12D23D34
a2=C01(C12(C34(D23J5+D45(J3+J4+J5))+C45(D23(J4+J5)+D34(J3+J4+J5))+D23D34D45)+C34(C45(D12(J3+J4+J5)+D23(J2+J3+J4+J5))+D12D23D45)+C45D12D23D34)+C12(C34(C45(D01(J3+J4+J5)+D23(J1+J2+J3+J4+J5))+D01D23D45)+C45D01D23D34)+C34C45D01D12D23
a1=C01(C12(C34(C45(J3+J4+J5)+D23D45)+C45D23D34)+C34C45D12D23)+C12C34C45D01D23
a0=C01C12C34C45D23
b7=D34J1J2J5
b6=(C34J1J2J5+D34(D01J2J5+D12J5(J1+J2)+D45J1J2))
b5=(C01D34J2J5+C12D34J5(J1+J2)+C34(D01J2J5+D12J5(J1+J2)+D45J1J2)+C45D34J1J2+D34(D01(D12J5+D45J2)+D12D45(J1+J2)))
b4=(C01(C34J2J5+D12D34J5+D34D45J2)+C12(C34J5(J1+J2)+D01D34J5+D34D45(J1+J2))+C34(C45J1J2+D01(D12J5+D45J2)+D12D45(J1+J2))+C45D34(D01J2+D12(J1+J2))+D01D12D34D45)
b3=(C01(C12D34J5+C34(D12J5+D45J2)+C45D34J2+D12D34D45)+C12(C34(D01J5+D45(J1+J2))+C45D34(J1+J2)+D01D34D45)+C34(C45(D01J2+D12(J1+J2))+D01D12D45)+C45D01D12D34)
b2=(C01(C12(C34J5+D34D45)+C34(C45J2+D12D45)+C45D12D34)+C12(C34(C45(J1+J2)+D01D45)+C45D01D34)+C34C45D01D12)
b1=(C01(C12(C34D45+C45D34)+C34C45D12)+C12C34C45D01)
b0=C01C12C34C45
Представить
передаточную функцию Wp(s) в виде произведения полиномов не выше второго
порядка в числителе и знаменателе Wp(s) в аналитическом виде не представляется
возможным даже теоретически, т.к. вид корней характеристических полиномов ai,bi,
а, следовательно, и вид разложения на полиномы не выше второго порядка,
зависит от численных значений параметров элементов модели. Поэтому исследование
влияния элементов модели на устойчивость ГС проводилось численно, путем
нахождения корней характеристических полиномов для каждого частного случая.
Далее по полученным корням определялись полиномы не выше второго порядка по
которым и строилась ЛАХ разомкнутой системы.
Все математические
операции проводилось с использованием пакета “MATHCAD” с помощью
которого численно определялись корни полиномов в передаточной функции
разомкнутой системы Wp(s), зная которые можно представить Wp(s) в виде
последовательного соединения элементарных звеньев. Это выполняется следующим
образом. Пусть полиномы числителя и знаменателя Wp(s) имеют корни lai, lbi соответственно. Эти корни могут быть нулевыми, действительными и
комплексно сопряженными. Каждый нулевой корень знаменателя lai=0 обеспечивает появление в составе
Wp(s) интегрирующего звена Wi(s)= 1/s, соответственно lbi=0 отвечает за появление чисто
дифференцирующего звена с Wi(s)= s. Каждый из действительных корней lai, lbi приносит в числитель или знаменатель соответственно выражение вида (Ti×s+1)×(1/Ti), где Ti=1/li , что соответствует появлению апериодических и
дифференцирующих звеньев в составе Wp(s). Каждая пара комплексно сопряженных
корней li, li* в составе
числителя или знаменателя передаточной функции отвечает за появление в
числителе или знаменателе соответственно выражений вида (Ti2 × s2 +2×xi×Ti×s +1)×(1/Ti2), где Ti=1
/ |li| , xi=Re(li) / |li|. Таким
образом, зная корни полиномов числителя и знаменателя передаточной функции
можно представить её в виде:
П(si)×П(Tg×s+1)×П( Tn2 × s2 +2×xn×Tn×s +1)
 Wp(s) = k × kw ×
(9) Wp(s) = k × kw ×
(9)
П(sj)×П(Tk×s+1)×П( Tm2 × s2 +2×xm×Tm×s +1)
П(1/Ti) × П(1/Ti2)
 где kw = где kw =
П(1/Ti) × П(1/Ti2)
Для численных
расчетов примем базовые параметры модели характерными для ГС данного типа,
которые равны следующим значениям:
J1 = 0.25 кг×м2 C01 =
1×103 Н×м/рад. D01=0.001
Н×м×с
J2 = 0.03 кг×м2 C12 =
1×103 Н×м/рад. D12=0.001
Н×м×с
J3 = 0.01 кг×м2 C23 =
0 D23=0.1 Н×м×с
J4 = 0.15 кг×м2 C34 =1×104 Н×м/рад. D34=0.001
Н×м×с
J5 = 1 кг×м2 C45
=1×103 Н×м/рад. D45=0.01
Н×м×с
К = 1000
Рассмотрим следующие
варианты модели:
1) ГС с “жесткими” рамами и
редуктором.
Начальные параметры
модели принимают следующие знечения:
J1 = 0.25 кг×м2 C01
= 1×1020 Н×м/рад. D01=
0.001 Н×м×с
J2 = 0.03 кг×м2 C12
= 1×1020 Н×м/рад. D12=
0.001 Н×м×с
J3 = 0.01 кг×м2 C23
= 0 D23=0.1 Н×м×с
J4 = 0.15 кг×м2 C34
=1×1020 Н×м/рад. D34=0.001
Н×м×с
J5 = 1 кг×м2 C45
=1×1020 Н×м/рад. D45=0.01
Н×м×с
К = 1000
Варьируем D23 = 0.01 ...
1 H×м×с
Передаточная функция
при этом имеет вид:
k × kw
 Wp(s)= (10) Wp(s)= (10)
s × (T×s+1)
Значения постоянной
времени Т, w, kw приведены
в Табл.1.
Табл.1.
|
D23
|
T
|
w=1/T
|
kw
|
|
0.01
|
116
|
0.0086
|
150
|
|
0.1
|
11.6
|
0.086
|
15
|
|
1
|
1.16
|
0.86
|
1.5
|
|
10
|
0.116
|
8.6
|
0.15
|
| 
 Главная
Главная
 Схемы
Схемы
 Студентам
Студентам
 Программы
Программы
 Поиск
Поиск
 Top50
Top50

 Главная
Главная
 Схемы
Схемы
 Студентам
Студентам
 Программы
Программы
 Поиск
Поиск
 Top50
Top50