Расчет настроек автоматического регулятора

Так как настройки регулятора не могут быть отрицательными то ограничимся 3 квадрантом. И с помощью программы на BASIC рассчитаем оптимальные настройки для ПИ - регулятора методом Стефани по следующим формулам:

          A^2(m,w)                                    m           1   

Tu = ------------------------ ,     kp = ---------- -  ----------

         w(m^2+1)* v(m,w)                 v(m,w)      u(m,w)

наибольшее отношение kp/Tu и будет оптимальными настройками.

Получили что kp = 1.712763

                        Tu = 4.47537

В программе SIAM с помощью схемы для одноконтурной системы без запаздывания получаем переходные процессы по заданию и по возмущению:

Сравнивая график кривой разгона по основному каналу и переходный процесс внутреннего контура каскадной системы делаем вывод о том, что за время запаздывания основного контура переходный процесс во внутреннем контуре затухнуть не успевает, следовательно передаточная функция эквивалентного объекта имеет вид:

                    Wоб(s) * Wp1(s)

Wоб(s) = --------------------------- =

                1 + Wоб1(s) * Wp1(s)

                  1                                              1

--------------------------------- * (1,7128 + ---------- )

               2                                               4,4754s    

 38,1160s + 10,6679s + 1

-------------------------------------------------------------- =

               0,4s + 1                                        1

1 + ---------------------------  * (1,7128 + ----------)      

                    2                                         4,4754s

      14,0904s + 6,9614s + 1

                   3                2

    107.9987s + 67.4444s + 14.6247s + 1

= ---------------------------------------------------------------------------

                    5                   4                3                  2  

   4116.4785s + 3186.9547s + 969.316s + 138.1861s + 15.7294s + 1

Определяем настройки ведущего регулятора. Для ПИ-регулятора получаем:

kp = 0.1249

Tu = 5.4148

В программе SIAM с помощью схемы каскадной системы получаем переходный процесс по заданию:

С помощью схемы каскадной системы получаем переходный процесс по возмущению:

б) для реальной передаточной функции.

Определим настройки внутреннего регулятора для объекта второго порядка с передаточной функцией

                         1

W1(s) =-------------------------

                            2

              16,1604s + 8.04s + 1

Получаем следующие настройки регулятора: kp = 4.3959

                                                                          Tu = 6.5957

В программе SIAM пользуясь схемой одноконтурной системы без запаздывания получаем графики переходных процессов по заданию и по возмущению:

Сравнивая график кривой разгона по основному каналу и переходный процесс внутреннего контура каскадной системы делаем вывод о том, что за время запаздывания основного контура переходный процесс во внутреннем контуре затухнуть не успевает, следовательно передаточная функция эквивалентного объекта имеет вид:

                Wоб(s) * Wp1(s)

Wоб(s) = --------------------------- =

                1 + Wоб1(s) * Wp1(s)

                  1                                              1

--------------------------------- * (4.3959 + ---------- )

           3             2                                     6.5957s    

91.125s + 60.75s + 13.5s + 1

-------------------------------------------------------------- =

               1                                            1

1 + ------------------------  * (4.3959 + ----------)      

                   2                                       6.5957s

      16.1604s + 8.04s + 1

                   3                  2

    468.5449s + 249.2673s + 37.0334s + 1

= --------------------------------------------------------------------------------------------

                6                     5                     4                   3                    2  

42696.154s + 49705.969s + 25770.6474s + 7229.3112s + 1076.6779s+71.4868s+  1

Определяем настройки ведущего регулятора. Для ПИ-регулятора получаем:

 kp = 1.2822

 Tu = 6.3952

В программе SIAM с помощью схем для каскадной системы получим переходные процессы по заданию и по возмущению:

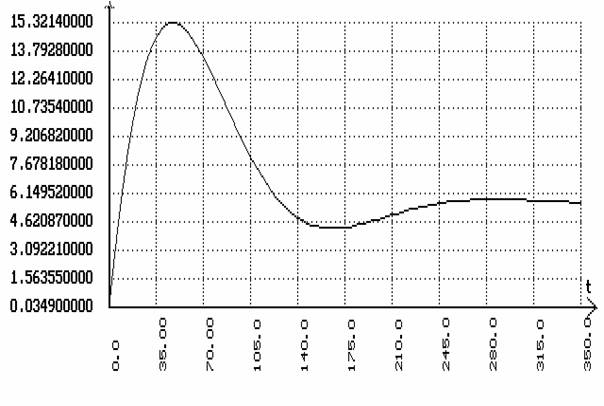
Расчет комбинированной АСР.

а) для эксперементальной передаточной функции

 Расчет компенсирующего устройства

В программе SIAM с помощью смоделированной схемы комбинированной системы без компенсатора получим соответствующий переходный процесс:

Определим передаточную функцию фильтра для структурной схемы где выход компенсатора поступает на вход регулятора по формуле:

               Wов(s)

Wф(s) = --------------------- ,

               Wоб(s) * Wр(s)

где Wов(s) - передаточная функция канала по возмущению,

      Wоб(s) - передаточная функция объекта,

     Wp(s) - передаточная функция регулятора

                    0,6887s + 1

                -----------------------------

                              2 

               30.8783 s + 10.2426 s + 1

Wф(s) = ---------------------------------------------------------- =

                                     1                                           1

               ------------------------------- * (1.0796 + ---------- )

                               2                                            8.0434 s

                38.8783 s + 10.6679 s + 1

                               4                 3                 2

               232.5099 s + 40.1406 s + 98.6173 s + 8.6837 s

           = -----------------------------------------------------------

                               3                  2

              268.1379 s + 119.8220 s + 18.9263 s + 1

Настроечные параметры компенсирующего устройства будут оптимальными, если АФХ фильтра равны нулю при нулевой и резонансной частоте.

б) для реальной передаточной функции

1	2	3	4	5	6	7	8	9	10	11

Copyright © Radioland. Все права защищены.
Дата публикации: 2004-09-01 (0 Прочтено)