Схемотехника аналоговых электронных устройств

В общем случае можно считать, что ОУ в активном фильтре корректирует АЧХ пассивного фильтра за счет обеспечения разных условий для прохождения различных частот спектра сигнала, компенсирует потери на заданных частотах, что приводит к получению крутых спадов выходного напряжения на склонах АЧХ. Для этих целей используются разнообразные частотно-избирательные ОС в ОУ. В активных фильтрах обеспечивается получение АЧХ всех разновидностей фильтров: нижних частот (ФНЧ), верхних частот (ФВЧ) и полосовых (ПФ).

Первым этапом синтеза всякого фильтра является задание передаточной функции (в операторной или комплексной форме), которая отвечает условиям практической реализуемости и одновременно обеспечивает получение необходимой АЧХ или ФЧХ (но не обеих) фильтра. Этот этап называют аппроксимацией характеристик фильтра.

Операторная функция представляет собой отношение полиномов:

K(p)=A(p)/B(p),

и однозначно определяется нулями и полюсами. Простейший полином числителя - константа. Число полюсов функции (а в активных фильтрах на ОУ число полюсов обычно равно числу конденсаторов в цепях, формирующих АЧХ) определяет порядок фильтра. Порядок фильтра указывает на скорость спада его АЧХ, которая для первого порядка составляет 20дБ/дек, для второго - 40дБ/дек, для третьего - 60дБ/дек и д.д.

Задачу аппроксимации решают для ФНЧ, затем с помощью метода инверсии частоты полученную зависимость используют для других типов фильтров. В большинстве случаев задают АЧХ, принимая нормированный коэффициент передачи:

,

где f(х) - функция фильтрации; - нормированная частота; - частота среза фильтра; e - допустимое отклонение в полосе пропускания.

В зависимости от того, какая функция принимается в качестве f(х) различают фильтры (начиная со второго порядка) Баттерворта, Чебышева, Бесселя и др. На рисунке 7.15 приведены их сравнительные характеристики.

Фильтр Баттерворта (функция Батерворта) описывает АЧХ с максимально плоской частью в полосе пропускания и относительно небольшой скоростью спада. АЧХ такого ФНЧ может быть представлена в следующем виде:

,

где n - порядок фильтра.

Фильтр Чебышева (функция Чебышева) описывает АЧХ с определенной неравномерностью в полосе пропускания, но не большей скоростью спада.

Фильтр Бесселя характеризуется линейной ФЧХ, в результате чего сигналы, частоты которых лежат в полосе пропускания, проходят через фильтр без искажений. В частности, фильтры Бесселя не дают выбросов при обработке колебаний прямоугольной формы.

Помимо перечисленных аппроксимаций АЧХ активных фильтров известны и другие, например, обратного фильтра Чебышева, фильтра Золотарева и т.д. Заметим, что схемы активных фильтров не изменяются в зависимости от типа аппроксимации АЧХ, а изменяются соотношения между номиналами их элементов.

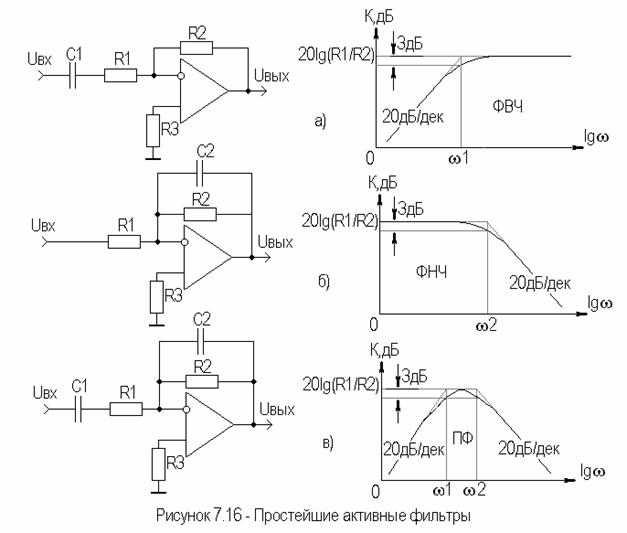
Простейшие (первого порядка) ФВЧ, ФНЧ, ПФ и их ЛАЧХ приведены на рисунке 7.16.

В этих фильтрах конденсатор, определяющий частотную характеристику, включен в цепь ООС.

Для ФВЧ (рисунок 7.16а) коэффициент передачи равен:

,

где .

Частоту сопряжения асимптот находят из условия , откуда

.

Для ФНЧ (рисунок 7.16б) имеем:

,

.

где .

В ПФ (рисунок 7.16в) присутствуют элементы ФВЧ и ФНЧ.

Можно увеличить крутизну спада ЛАЧХ, если увеличить порядок фильтров. Активные ФНЧ, ФВЧ и ПФ второго порядка приведены на рисунке 7.17.

Наклон асимптот у них может достигать 40дБ/дек, а переход от ФНЧ к ФВЧ, как видно из рисунков 7.17а,б, осуществляется заменой резисторов на конденсаторы, и наоборот. В ПФ (рисунок 7.17в) имеются элементы ФВЧ и ФНЧ. Передаточные функции равны [13]:

¨ для ФНЧ:

;

¨ для ФВЧ:

;

¨ для ПФ:

.

Для ПФ резонансная частота равна:

.

Для ФНЧ и ФВЧ частоты среза соответственно равны:

;

.

Довольно часто ПФ второго порядка реализуют с помощью мостовых цепей. Наиболее распространены двойные Т-образные мосты, которые "не пропускают" сигнал на частоте резонанса (рисунок 7.18а) и мосты Вина, имеющие максимальный коэффициент передачи на резонансной частоте (рисунок 7.18б).

Мостовые схемы включены в цепи ПОС и ООС. В случае двойного Т-образного моста глубина ООС минимальна на частоте резонанса, и усиление на этой частоте максимально. При использовании моста Вина, усиление на частоте резонанса максимально, т.к. максимальна глубина ПОС. При этом для сохранения устойчивости глубина ООС, введенной с помощью резисторов и , должна быть больше глубины ПОС. Если глубины ПОС и ООС близки, то такой фильтр может иметь эквивалентную добротность Q»2000.

Резонансная частота двойного Т-образного моста при и , и моста Вина при и , равна , и ее выбирают исходя из условия устойчивости , т.к. коэффициент передачи моста Вина на частоте равен 1/3.

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	45